При использовании сортировки с помощью дерева явно строится двоичное дерево сравнения ключей. Построение дерева начинается с листьев, которые содержат все элементы массива. Из каждой соседней пары выбирается наименьший элемент, и эти элементы образуют следующий (ближе к корню уровень дерева). Из каждой соседней пары выбирается наименьший элемент и т.д., пока не будет построен корень, содержащий наименьший элемент массива. Двоичное дерево сравнения для массива, используемого в наших примерах, показано на рисунке 1. Итак, мы уже имеем наименьшее значение элементов массива. Для того, чтобы получить следующий по величине элемент, спустимся от корня по пути, ведущему к листу с наименьшим значением. В этой листовой вершине проставляется фиктивный ключ с "бесконечно большим" значением, а во все промежуточные узлы, занимавшиеся наименьшим элементом, заносится наименьшее значение из узлов - непосредственных потомков (рис. 2). Процесс продолжается до тех пор, пока все узлы дерева не будут заполнены фиктивными ключами (рисунки 3 - 8).

Рис. 1.

Рис. 2. Второй шаг

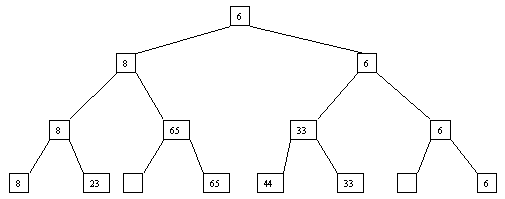
Рис. 3. Третий шаг

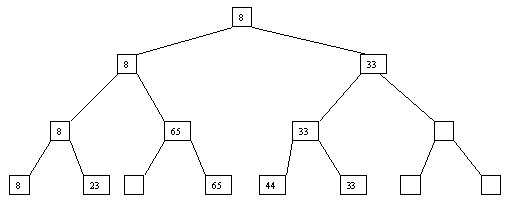
Рис. 4. четвертый шаг

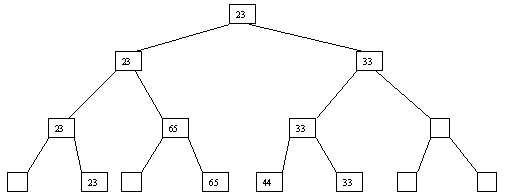
Рис. 5. Пятый шаг

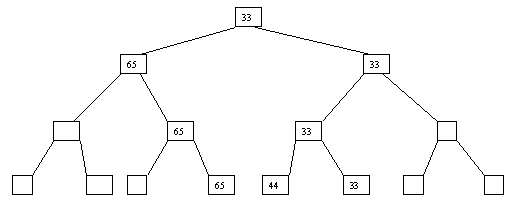
Рис. 6. Шестой шаг

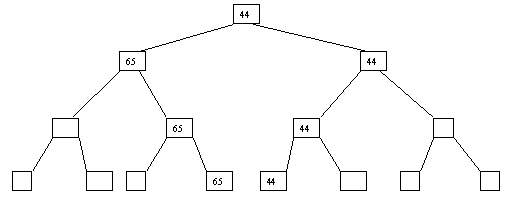
Рис. 7. Седьмой шаг

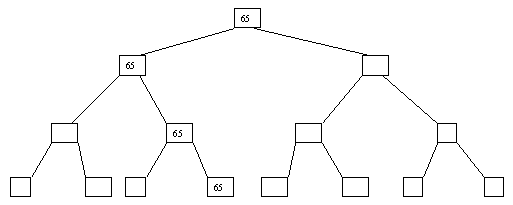
Рис. 8. Восьмой шаг

На каждом из n шагов, требуемых для сортировки массива, нужно log n (двоичный) сравнений. Следовательно, всего потребуется n?log n сравнений, но для представления дерева понадобится 2n - 1 дополнительных единиц памяти.

Имеется более совершенный алгоритм, который принято называть пирамидальной сортировкой (Heapsort). Его идея состоит в том, что вместо полного дерева сравнения исходный массив a[1], a[2], ..., a[n] преобразуется в пирамиду, обладающую тем свойством, что для каждого a[i] выполняются условия a[i] <= a[2i] и a[i] <= a[2i+1]. Затем пирамида используется для сортировки.

Наиболее наглядно метод построения пирамиды выглядит при древовидном представлении массива, показанном на рисунке 9. Массив представляется в виде двоичного дерева, корень которого соответствует элементу массива a[1]. На втором ярусе находятся элементы a[2] и a[3]. На третьем - a[4], a[5], a[6], a[7] и т.д. Как видно, для массива с нечетным количеством элементов соответствующее дерево будет сбалансированным, а для массива с четным количеством элементов n элемент a[n] будет единственным (самым левым) листом "почти" сбалансированного дерева.

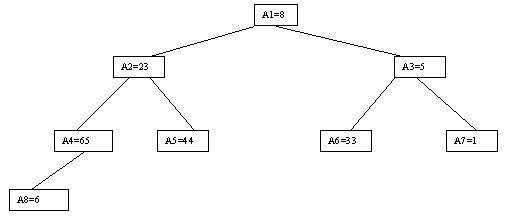
Рис. 9.

Очевидно, что при построении пирамиды нас будут интересовать элементы a[n/2], a[n/2-1], ..., a[1] для массивов с четным числом элементов и элементы a[(n-1)/2], a[(n-1)/2-1], ..., a[1] для массивов с нечетным числом элементов (поскольку только для таких элементов существенны ограничения пирамиды). Пусть i - наибольший индекс из числа индексов элементов, для которых существенны ограничения пирамиды. Тогда берется элемент a[i] в построенном дереве и для него выполняется процедура просеивания, состоящая в том, что выбирается ветвь дерева, соответствующая min(a[2?i], a[2?i+1]), и значение a[i] меняется местами со значением соответствующего элемента. Если этот элемент не является листом дерева, для него выполняется аналогичная процедура и т.д. Такие действия выполняются последовательно для a[i], a[i-1], ..., a[1]. Легко видеть, что в результате мы получим древовидное представление пирамиды для исходного массива (последовательность шагов для используемого в наших примерах массива показана на рисунках 10-13).

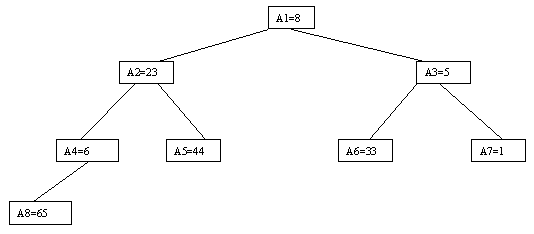
Рис. 10.

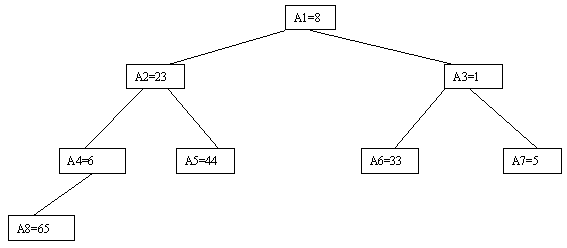
Рис. 11.

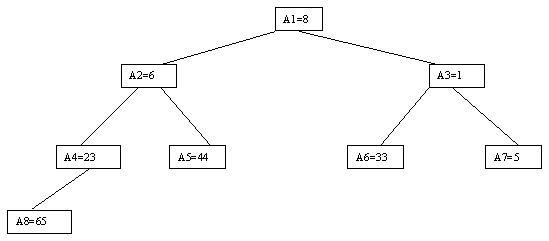
Рис. 12.

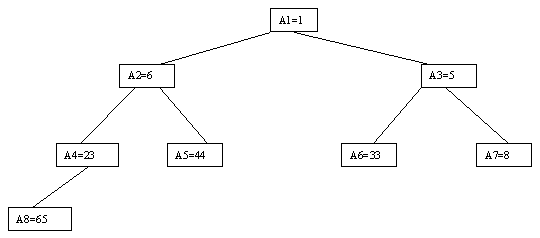
Рис. 13.

          Алгоритм очень  эффективен  для  большого  числа  элементов  n; чем  больше  n, тем лучше она  работает.

         В  худшем  случае  нужно  n/2  сдвигающих  шагов, они  сдвигают  элементы  на  log(n/2), log(n/2 – 1), … ,log(n – 1)  позиций  (логарифм  по  [основанию 2]  «обрубается»  до  следующего  меньшего  целого). Следовательно  фаза  сортировки  будет  n – 1  сдвигов  с  самое  большое  log(n-1), log(n-2), … , 1  перемещениями.

Можно  сделать  вывод, что  даже  в  самом  плохом  из  возможных  случаев  алгоритму  потребуется  n*log n  шагов.